1. Basic Concepts
|
| |
| 1.1 Allocation and deallocation of memory |
| |
int main()
{
int i, *pi;
if ( !(pi = (int *)malloc(sizeof(int))) )
{
fprintf(stderr, “Insufficient memory”);
exit(0);
}
*pi = 3;
printf(“%d\n”, *pi);
free(pi);
return 0;
} |
|
| |
| 1.2 Algorithm Specification |
| |
 Definition: An algorithm is a finite set of instructions that, if followed, accomplishes a particular task. In addition, all algorithms must satisfy the following criteria. Definition: An algorithm is a finite set of instructions that, if followed, accomplishes a particular task. In addition, all algorithms must satisfy the following criteria. |
1) Input. There are zero or more quantities that are externally supplied.
2) Output. At least one quantity is produced.
3) Definiteness. Each instruction is clear and unambiguous.
4) Finiteness. If we trace out the instructions of an algorithm, then for all cases, the algorithm terminates after a finite number of steps.
5) Effectiveness. Every instruction must be basic enough to be carried out, in principle, by a person using only pencil and paper. It is not enough that each operation be definite as in 3); it also must be feasible. |
| |
 In computational theory, one distinguishes between an algorithm and a program, the latter of which does not have to satisfy the fourth condition. For example, we can think of an operating system that continues in a wait loop until more jobs are entered. In computational theory, one distinguishes between an algorithm and a program, the latter of which does not have to satisfy the fourth condition. For example, we can think of an operating system that continues in a wait loop until more jobs are entered. |
| |
| Example |
| |
 [Selection sort] Suppose we must devise a program that sorts a set of n ≥ 1 integers. [Selection sort] Suppose we must devise a program that sorts a set of n ≥ 1 integers.
 STEP 1. From those integers that are currently unsorted, find the smallest and place it next in the sorted list. STEP 1. From those integers that are currently unsorted, find the smallest and place it next in the sorted list.
 STEP 2. Write it partially in C and partially in English STEP 2. Write it partially in C and partially in English |
| |
for (i=0; i<n; i++)
{
Examine list[i] to list[n-1] and suppose that
the smallest integer is at list[min];
Interchange list[i] and list[min];
} |
|
| |
#include <stdio.h>
#include <stdlib.h> // rand()
#define SWAP(x, y, t) ((t)=(x), (x)=(y), (y)=(t))
void sort(int list[], int n);
int main(void)
{
int i, list[100];
for (i=0; i<100; i++) list[i] = rand() % 1000;
sort(list, i);
for (i=0; i<100; i++) printf("%d\n", list[i]);
return 0;
}
void sort(int list[], int n)
{
int i, j, min, temp;
for (i=0; i<n-1; i++) {
min = i;
for (j=i+1; j<n; j++)
if (list[j]<list[min]) min = j;
SWAP(list[i], list[min], temp);
}
} |
|
| |
| 1.3 Performance Analysis |
| |
 One of the goals of this course to develop your skills for making evaluative judgments about programs. One of the goals of this course to develop your skills for making evaluative judgments about programs. |
1) Does the program meet the original specifications of the task?
2) Doest it work correctly?
3) Doest the program contain documentation that shows how to use it and how it works?
4) Doest the program effectively use functions to create logical units?
5) Is the program’s code readable?
6) Does the program efficiently use primary and secondary storage?
7) Is the program’s running time acceptable for the task? |
 These criteria focus on performance evaluation, we can loosely divide into two distinct fields: These criteria focus on performance evaluation, we can loosely divide into two distinct fields:
space complexity and time complexity. |
| |
| 1.3.1 Space Complexity |
| |
 The amount of memory that it needs to run to completion. The amount of memory that it needs to run to completion. |
 Fixed space requirement Fixed space requirement |
– Space requirements that do not depend on the number and size of the program’s input and outputs.
– Include the instruction space, space for simple variables, fixed-size structured variables (such as structs), and constants. |
 Variable space requirement Variable space requirement |
– The space needed by structured variables whose size depends on the particular instance, I, for the problem being solved.
– Include the additional space required when a function uses recursion. |
 The total space requirement = fixed + variable The total space requirement = fixed + variable |
| S(P) = c + SP(I) |
– c: constant representing the fixed space requirements.
– SP(I) : the variable space requirement of a program P working on an instance I. It is represented by SP(n) if n is the only instance characteristic of the instance I. |
| |
| Example: summing a list of numbers |
| |
 Iterative function: Ssum(n) = 0 Iterative function: Ssum(n) = 0 |
float sum(float list[], int n)
{
int i; float tempsum = 0;
for (i=0; i<n; i++) tempsum += list[i];
return tempsum;
} |
|
| |
 Recursive function: Srsum(n) = 12*n bytes Recursive function: Srsum(n) = 12*n bytes |
float rsum(float list[], int n)
{
if (n) return rsum(list, n-1) + list[n-1];
return 0;
} |
|
| |
| Type |
Name |
Number of bytes |
| array pointer |
list[ ] |
4 |
| integer |
n |
4 |
| return address |
|
4 |
| Total per recursive call |
|
12 |
|
| |
| 1.3.2 Time Complexity |
| |
 The amount of computer time that it needs to run to completion. The amount of computer time that it needs to run to completion.
 The time, T(P) taken by a program, P, The time, T(P) taken by a program, P,
T(P) = compile time + TP(I) |
– The compile time is similar to the fixed space component.
– TP(I): program run (or execution) time |
 Machine-dependent estimate of TP(I) Machine-dependent estimate of TP(I) |
– Not easy task because it
– Letting n denote the instance characteristic, we might express
TP(n) = caADD(n) + csSUB(n) + clLDA(n) + cstSTA(n)
– where are constants that refer to the time needed to perform each operation, and ADD, SUB, LDA, STA are number of additions, subtractions, loads, and stores that are performed.
|
 Machine-independent estimate of TP(I) Machine-independent estimate of TP(I) |
– Program step
|
| |
| Program Step |
| |
 Definition: A program step is a syntactically or semantically meaningful program segment whose execution time is independent of the instance characteristics. Definition: A program step is a syntactically or semantically meaningful program segment whose execution time is independent of the instance characteristics. |
| |
 Step count for summing Step count for summing |
| |

|
| |
 Step count for recursive summing Step count for recursive summing |
| |
 |
| |
 Step count for summing Step count for summing |
| |
 |
| |
| 1.4 Asymptotic Notation |
| |
 Definition: [Big “oh”] f(n) = O(g(n)) (read as “f of n is big oh g of n”) iff (if and only if) there exist positive constants c and n0 such that f(n) ≤ cg(n) for all n, n ≥ n0. Definition: [Big “oh”] f(n) = O(g(n)) (read as “f of n is big oh g of n”) iff (if and only if) there exist positive constants c and n0 such that f(n) ≤ cg(n) for all n, n ≥ n0. |
| |
| Example |
| |
| 3n+2 = O(n) |
3n+2 ≤ 4n for all n ≥ 2 |
| 100n+6 = O(n) |
100n+6 ≤ 101n for all n ≥ 10 |
| 10n2+4n+2 = O(n2) |
10n2+4n+2 ≤ 11n2 for all n ≥ 5 |
| 6*2n+n2 = O(2n) |
6*2n+n2 ≤ 7*2n for all n ≥ 4 |
|
| |
| O(1) |
a computing time is constant |
| O(n) |
linear |
| O(n2) |
quadratic |
| O(n3) |
cubic |
| O(2n) |
exponential |
|
| |
 The seven computing times The seven computing times |
– O(1), O(log n), O(n), O(n log n), O(n2), O(n3), O(2n)
|
| |
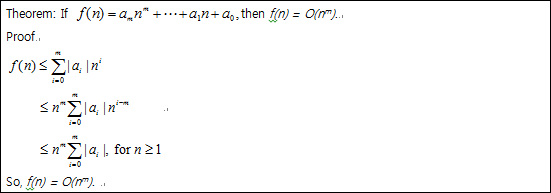 |
| |
| 1.5 Performance Measurement |
| |
 We discuss on measuring time. We discuss on measuring time.
 There are actually two different methods for timing events in C, by using C’s standard library accessed through #include <time.h> There are actually two different methods for timing events in C, by using C’s standard library accessed through #include <time.h> |
 Method 1: clock() Method 1: clock() |
– This function gives the amount of processor time, as the built-in type clock_t, that has elapsed since the program began running.
|
 Method 2: time() Method 2: time() |
– This function returns the time, measured in seconds, as the built-in type time_t.
|
| |
|
Method 1 |
Method 2 |
| Start timing |
start = clock(); |
start = time(NULL); |
| Stop timing |
stop = clock(); |
stop = time(NULL); |
| Type returned |
clock_t |
time_t |
| Result in seconds |
duration =
((double)(stop-start))
/CLOCKS_PER_SEC; |
duration =
(double)
difftime(stop, start); |
|
| |
| Example: timing program for worst-case sorting |
| |
 O(n) vs O(n2) O(n) vs O(n2) |
#include <stdio.h>
#define MAX_SIZE 1001
void sort(int list[], int n);
int main(void)
{
int i, n, step = 10;
int a[MAX_SIZE];
double duration;
clock_t start;
for (n=0; n<MAX_SIZE; n+=step) {
for (i=0; i<n; i++)
a[i] = n-i;
start = clock();
sort(a, n);
duration = ((double)(clock()-start))/CLOCK_PER_SEC;
printf(“%d\t%f\n”, n, duration);
if (n==100)
step = 100;
}
return 0;
} |
|
| |