3. Sort
|
| |
| 3.1 Bubble Sort |
| |
 Bubble sort is a simple sorting algorithm. Although the algorithm is simple, it is not efficient for sorting large lists; other algorithms are better.
Analysis: O(n2) |
| |
void bubble_sort(int list[], int n)
{
int i, j;
for (i=0; i<n; i++) {
for (j=n-1; j>i; j--)
if (list[j-1]>list[j])
swap(&list[j-1], &list[j]);
}
}
|
|
| |
| 3.2 Insertion Sort |
| |
| Algorithm |
– Every repetition of insertion sort removes an element from the input data, inserting it into the correct position in the already-sorted list, until no input elements remain.
– In each iteration the first remaining entry of the input is removed, inserted into the result at the correct position, thus extending the result: |
 |
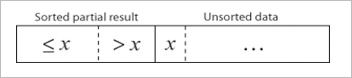| becomes |
 |
| |
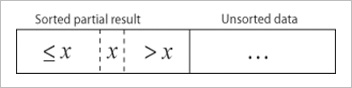void insertion_sort(int list[], int n)
{
int i, j;
int temp;
for (j=1; j<n; j++) {
temp = list[j];
i = j-1;
while (i>=0 && list[i]>temp) {
list[i+1] = list[i];
i--;
}
list[i+1] = temp;
}
} |
|
| |
|
|
| |
| Analysis: O(n2) |
 |
| |
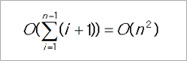| 3.3 Quick Sort |
| |
Quick sort is a sorting algorithm developed by Tony Hoare that, on average.
Analysis: In the average O(n log n) and in the worst case, O(n2). |
| ① Quick sort is often faster in practice than other O(n log n) algorithms. |
| Algorithm |
| - The steps are: |
① When n<=1, the list is sorted.
When n>1, select a pivot element from out of n elements.
② Partition the n elements into 3 segments left, middle, and right.
The middle segment contains only the pivot element.
All elements in the left segments are <= pivot.
All elements in the right segments are >= pivot.
③ Sort left and right segments recursively. |
| - Answer is sorted left segment, followed by middle segment followed by sorted right segment. |
| |
| Example |
| |
| list |
 |
① Select a pivot as list[left] = 6
② Partition |
 |
| ③ Sort left and right segments recursively. |
| |
| Choice of pivot |
| |
| Left most element |
– Pivot is left most element in list that is to be sorted.
– When sorting list[6:20], use list[6] as the pivot. |
| Random selection§ |
– Randomly select any one such that left <= pivot <= right
– When sorting list[6:20], generate a random number r in the range [6, 20]. Use list[r] as the pivot. |
| Median-of-three rule |
– Select the one with median key as the pivot.
– When sorting list[6:20], examine list[6], list[(6+20)/2], and list[20]. Select the element with median (i.e., middle) key.
– If list[6] = 30, list[13] = 2, and list[20] = 10, list[20] becomes the pivot.
– If list[6] = 3, list[13] = 2, and list[20] = 10, list[6] becomes the pivot. |
| |
| C code (version 1) |
void quick_sort(int list[], int left, int right)
{
int pivot, i, j;
if (left < right) {
// select a pivot
pivot = list[left];
// partition
i = left;
j = right+1;
do {
do i++; while (list[i] < pivot);
do j--; while (list[j] > pivot);
if (i < j) swap(&list[i], &list[j]);
} while (i < j);
swap(&list[left], &list[j]);
// sort left and right segments recursively
quick_sort(list, left, j-1);
quick_sort(list, j+1, right);
}
} |
| |
|
| |
| C code (version 2) |
void quick_sort(int list[], int left, int right)
{
int pivot, i, mid;
if (left < right) {
// pivot is midpoint; move to left side
swap(&list[left], &list[(left+right)/2]);
pivot = list[mid=left];
// partition
// left side < pivot (left+1 to mid),
// right side >= pivot (mid+1 to right)
for (i=left+1; i<=right; i++) {
if (list[i] < pivot)
swap(&list[i], &list[++mid]);
}
// resotre pivot position
swap(&list[left], &list[mid]);
if (mid > left) quick_sort(list, left, mid-1);
if (mid < right) quick_sort(list, mid+1, right);
}
} |
|
| |
| Average Complexity |
| |
| If T(n) is the time taken to sort a list of n records, then when the list splits roughly into two equal parts each time a record is positioned correctly, we have |
 |
| |
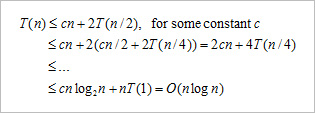| 3.4 Comparison of Sort Methods |
| |
| Name |
Best |
Average |
Worst |
| Bubble sort |
n |
n2 |
n2 |
| Insertion sort |
n |
n2 |
n2 |
| Quick sort |
n log n |
n log n |
n2 |
| Merge sort |
n log n |
n log n |
n log n |
| Heap sort |
n log n |
n log n |
n log n |
|
| |